1. 论文介绍
论文题目:Over-Squashing in GNNs and Causal Inference of Rewiring Strategies
论文发表:2025-08 Arxiv,Accepted at CIKM 2025
论文领域:图神经网路,图重连算法
论文代码:https://github.com/Danial-sb/Over-Squashing-Measurement
论文背景:

2. 论文摘要
图形神经网络(GNNs)在推荐系统、材料设计和药物再利用等领域表现出了最先进的性能。然而,消息传递的GNN受到过度挤压的影响——来自远程节点的远程信息的指数压缩——这限制了表达能力。重布线技术可以缓解这一瓶颈;但由于缺乏直接的经验过度挤压度量,其实际影响尚不清楚。我们提出了一个严格的,拓扑集中的方法来评估过度挤压之间的节点对使用衰减率的相互敏感性。然后,我们将这些成对评估扩展到四个图形级统计(患病率、强度、变异性、极端性)。将这些度量与图内因果设计相耦合,我们量化了重布线策略如何影响不同图和节点分类基准上的过度挤压。我们大量的实证分析表明,大多数图分类数据集都会遭受过度挤压(但程度不同),而重新布线有效地缓解了过度挤压——尽管减轻程度及其转化为性能增益的程度因数据集和方法而异。我们还发现,在节点分类数据集中,过度挤压不太显著,重新布线通常会增加过度挤压,并且性能变化与过度挤压变化不相关。这些发现表明,当过度挤压是实质性的,并且有限制地纠正时,重新布线是最有益的——而过度侵蚀性的重新布线,或者应用于最小程度地过度挤压的图形的重新布线,不太可能有助于甚至可能损害性能。我们的即插即用诊断工具让从业者在接受任何培训之前决定重新布线是否有可能奏效。
3. 相关介绍
3.1 过度挤压程度的定义
感受野随着层数的增加呈指数级增长,迫使 MPNN 将越来越大的节点特征集压缩为固定宽度的节点嵌入。这种过度压缩会导致信息丢失并降低模型的表达能力
信息的过度压缩可以通过评估通过绝对雅可比范数传递到节点 u 输入特征$h_u^{(0)}$ 的层后L节点$v$表示的敏感性来理解
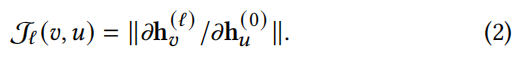
标准化的雅可比范围为
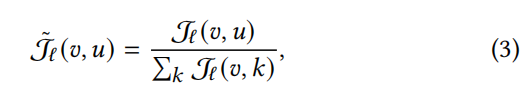
节点 v 在层 L 上的特征对节点 u 初始特征的敏感性,相 v 对于对所有节点的敏感性。如果没有这种归一化,模型可能会仅根据节点的绝对雅可比范数高估节点的灵敏度。L(v,u) 表示节点 v 对节点的敏感性,可以忽略不计 u ,表示过度挤压。
3.2 过度挤压的衡量
雅可比规范(及其变体)是过度压扁的原则性衡量标准,但也有实际缺陷。
缺陷:
(i)它在计算上是令人望而却步的:对于具有特征维度的节点 d , n 完整的雅可比是一个 (nd)×(nd) 矩阵,需要 O(n2d2) 内存和时间。
(ii) 它依赖于参数 ,随权重更新和特定于模型的超参数(例如,隐藏大小)而变化。
(iii)它无法隔离图的拓扑效应,高度依赖于模型选择和参数。
具有高有效电阻的节点对更容易受到过度挤压,并且整个图的总有效电阻可作为过度挤压的全局代表。
然而,有效电阻的局限性:
(a) 它只允许相对比较——没有为何时或多严重地发生过度挤压提供阈值;
(b) 尽管与过度挤压有关,但有效电阻并非来自其形式表征,给定对是否真的被过度压扁存在不确定性。
为了避免这些缺点,我们直接近似相对雅可比范数,从而产生一个既以拓扑为中心又在很大程度上与模型无关的度量,而无需全雅可比计算的大量计算成本。
4. 测量和因果关系框架
本文提出了一种有理论依据的、以拓扑为重点的方法来测量图中节点对的成对过度挤压程度,并将其扩展到在图级别的可量化的过度挤压的衡量单位。通过我们的图级测量,本文评估了现有一些图重连算法在减轻过度挤压方面的因果效应。
4.1 节点间的过度挤压衡量
该衡量指标的目标是在图中的节点对之间推导出成对的过度挤压度量,该度量是
(i) 每个图计算一次,
(ii) 与相对雅可比范数保持一致,作为测量过度挤压的基础,
(iii) 专注于图拓扑,
(iv) 仅依赖于模型深度作为影响因素,
(v) 理论上基于过度压扁的严格定义。我们通过引入相对雅可比范数的近似值来实现 (i–iv),以及 (v) 通过考虑指数衰减率来实现。
4.2 归一化雅可比范数的近似值
为了量化过度挤压,我们关注相对雅可比范数,L(v,u) 因为它将节点 v 对节点 u 的敏感性捕获为其对所有节点的总敏感性的一小部分,解决了绝对范数的局限性 L(v,u) ,它不考虑接收到的信息 v 总量。 L(v,u) 由于雅可比计算的成本,以及随着模型参数和超参数(例如权重、隐藏维等)的变化而重新计算的要求,计算成本高得令人望而却步。
此外,这些依赖关系模糊了过度压缩的拓扑原因及其模型级效应。为了解决所有这些计算和依赖问题,我们引入了归一化雅可比范数的近似值。
4.3 图级过度挤压的测量
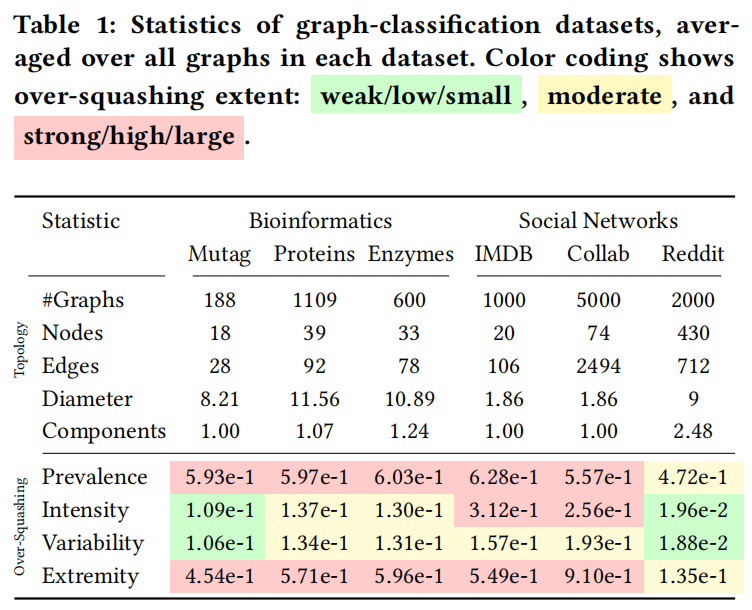
为了得出图级评估,我们使用四个统计数据总结了正衰减率的分布:
- 患病率(Prevalence)是衰减率为正的节点对的分数 ( $k_{vu}$>0 )。它反映了过度压缩在图中的分布。
- 强度(Intensity)是所有正衰减率的平均值,表示受影响节点对之间过度压扁的典型强度。
- 变异性(Variability)是正衰减率的标准差,用于衡量节点对之间过度挤压强度的一致性或差异。
- 端(Extremity)是图中观察到的最大正衰减率,捕获了最坏情况下的过度挤压实例。
4.4 图重连算法效应的因果估计
为了确保将过度挤压指标的差异与重新布线的有效因果关系归因,我们采用了标准的因果推断假设:SUTVA、阳性、可交换性和一致性。
G 通过个体处理效应(ITE)评估重新布线如何 R 影响图表的过度挤压测量 M:
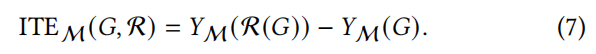
具有图形数据 N 集的图形分类任务 𝒟={Gi} ,我们测量平均处理效果 (ATE) 以捕获 R 跨数据集图重连算法的总体影响:
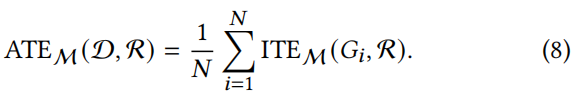
对于每个数据集,我们分析了所有四个图级测量值,以评估重新布线 ℛ 对图中过度压扁的患病率、强度、变异性和极端性的影响。
5. 实验设置
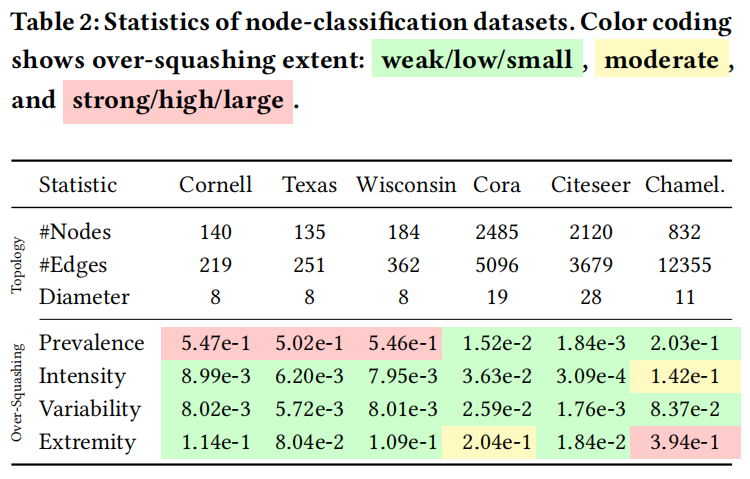
首先测量各种数据集中的过度挤压的水平衡量度。然后,使用本文的因果框架,我们评估了图重连算法在减少图和节点分类基准上的过度压扁方面的有效性。
图形分类数据集的统计信息,对每个数据集中的所有图形进行平均。颜色编码显示过度挤压程度: 弱/低/小 、 中和强/高/大
6. 总结
通过研究过度挤压问题,自己给出了一个新的定义指标来描述局部和全局的过度挤压程度,并与不同数据集的关联,和不同算法之间的比较。最终在一个CCF-B类会议上接受。
7. 个人感想
不仅仅是提出新的算法,给出新的衡量方式,提出新的观点和概念都是可以发出来。