淮南市网站建设_网站建设公司_C#_seo优化

此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第五课的第二周内容，2.1和2.3的内容以及一些基础的补充。

---

本周为第五课的第二周内容，与 CV 相对应的，这一课所有内容的中心只有一个：自然语言处理（Natural Language Processing，NLP）。
应用在深度学习里，它是专门用来进行文本与序列信息建模的模型和技术，本质上是在全连接网络与统计语言模型基础上的一次“结构化特化”，也是人工智能中最贴近人类思维表达方式的重要研究方向之一。
这一整节课同样涉及大量需要反复消化的内容，横跨机器学习、概率统计、线性代数以及语言学直觉。
语言不像图像那样“直观可见”，更多是抽象符号与上下文关系的组合，因此理解门槛反而更高。
因此，我同样会尽量补足必要的背景知识，尽可能用比喻和实例降低理解难度。
本周的内容关于词嵌入，是一种相对于独热编码，更能保留语义信息的文本编码方式。通过词嵌入，模型不再只是“记住”词本身，而是能够基于语义关系进行泛化，在一定程度上实现类似“举一反三”的效果。词嵌入是 NLP 领域中最重要的基础技术之一。

本篇的内容关于词汇表征和类比推理，是词嵌入中的基础内容。

1.词汇表征

先用一句话简单概括一下：词汇表征的含义是将词汇表示为多维特征向量，以便模型对词语进行计算与比较。
这也是词嵌入方法所遵循的核心思想之一，下面就来详细展开：

1.1 独热编码在序列编码中的局限

在上周的引入中，我们就对独热编码在序列编码中的一些局限有所提及，再简单重复一下：独热向量的维度极高、且极度稀疏带来了极高的存储和计算成本，这一问题在词典规模越大的任务中便越被凸显。

但我们知道，这种成本上的问题往往并不是根本问题所在，有时甚至可以忽略，我们关注一门技术好不好，更多的是在乎它的“效益”，也就是对最终性能的提升。
因此，在序列信息的表示上，独热编码的核心局限并非成本，而是它限制了文本的语义表示，无法显式建模词语之间的语义关系。
这点并不难理解，我们用课程里的例子来说明一下：

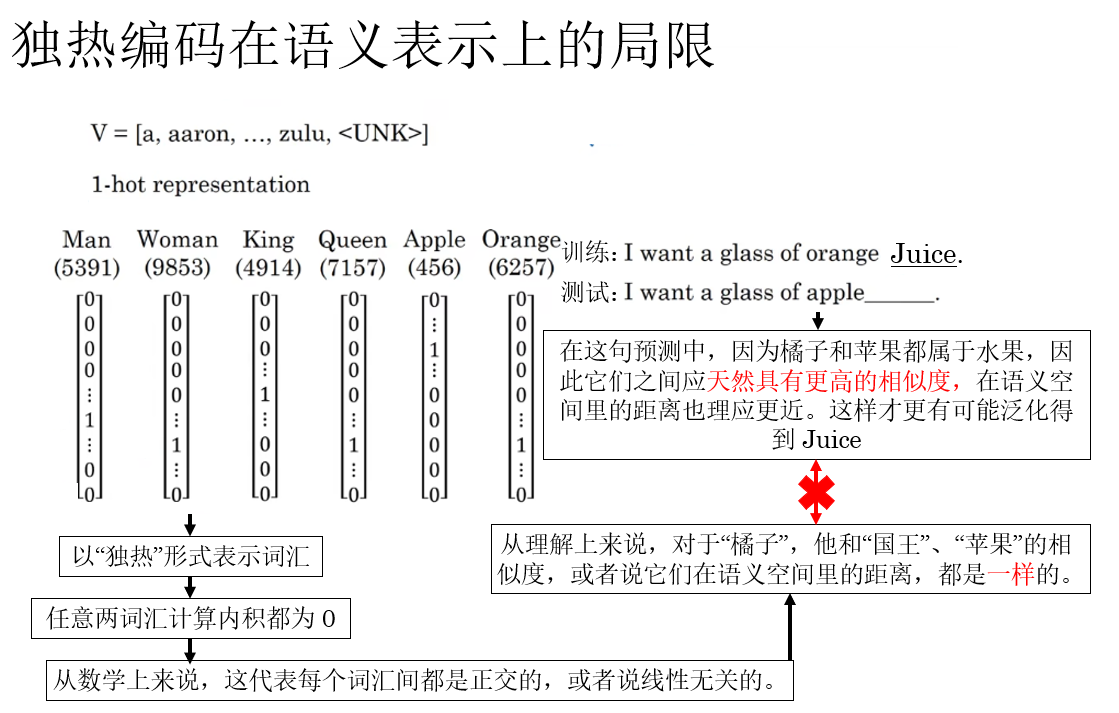
就像图里所示，换句话来总结：独热编码将各个词汇“孤立”了，断绝了苹果和橘子、父亲和母亲、男人和女人这样的词汇间的联系。
显然，这对模型泛化能力的影响是极大的，这也是独热编码在序列表示中的核心问题所在。

这个问题的解决方法就是使用词汇表征。

1.2 词汇的特征化表示

这点同样很符合我们的语言直觉，既然我们知道各个词汇间存在共性、存在某些维度上的相似，那就像归纳总结把它们列举出来，就像这样：
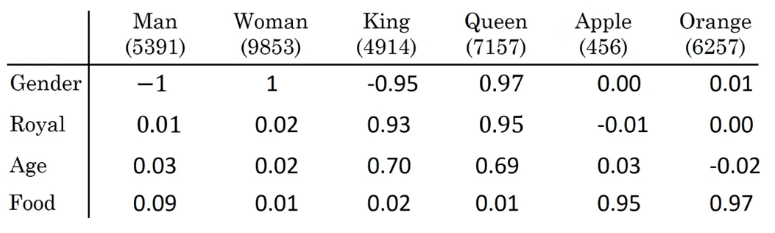以性别特征为例简单解释一下：我们将男性设置为 -1，把女性设置为 1，以此为尺度估量其他词汇在性别维度上的值，就可以发现，国王在该维度上更接近男性，而王后则更接近女性，在这种示意下，苹果等与性别无关或不以性别为核心特征的词汇在该维度上的值则接近 0 。

但是，这里要专门强调一点：这些特征不是我们人为手工定义的，我们这里只是以此进行演示。在实际运行中，词汇在各个维度上的值是通过相应的网络学习并输出的，其各个维度上的语义并不具备这样较强的可解释性。
在之后我们也会详细展开相关内容。

在这一部分，吴恩达老师还提及了一种算法：t-SNE 算法，这种算法是一种把高维向量“摊平”到 2D / 3D 平面上，并尽量保留“局部相似关系”的可视化方法，我们可以以此来可视化各个词汇在向量空间中的大致距离，就像这样：

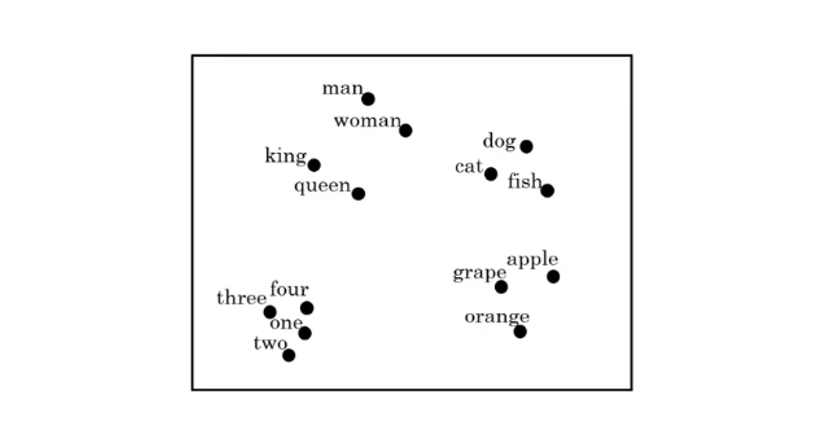
这个算法的原理涉及到很多没提到过的数学概念，详细介绍需要大量篇幅，而且目前也有了很多理论更优的同类型方法，因此就不在这里展开了，以后如果有机会再专门介绍这类内容，这里附上原论文链接：Visualizing Data using t‑SNE

最终，通过一个词汇在多个维度上的表示，我们就通过另一种方式实现了对词汇的编码。
这种表示方式能够通过向量间的距离度量词汇语义相似性，从而提升模型的理解与泛化能力，同时也避免了独热编码维度过高且表示稀疏的问题。

假设我们规定使用 300 维的特征向量来编码词汇时，我们便称这个特征向量为词向量。
同时，这样一个个词向量就像是“嵌入”在了这样一个 300 维的向量空间里。所以，当我们将词汇表示为低维连续向量，并将其映射到同一向量空间中进行学习与比较时，这种表示方式就被称为词嵌入（embedding）。

我们之后就会详细展开实现词嵌入相关的技术和模型。
下面我们简单展开一下词嵌入实现的另一项应用：类比推理。

2. 使用词嵌入进行类比推理

在我们实现了词嵌入，得到词表中词汇的词向量表示后，我们可以通过一种方式来观察和验证词嵌入的语义能力，就是类比推理。
在 2013年，一篇名为Linguistic Regularities in Continuous Space Word Representations的论文就详细展示了词向量能反映语言类比现象的数据分析方法，同时，我们之后要介绍的 Word2Vec 中也展示了词向量可以实现类比推理。
总之,词嵌入中的类比推理通过向量运算验证和展示词向量的语义规律性，既体现了词嵌入空间的线性结构，也能直观反映模型对语言关系的理解能力。

同样用一句话简单概括一下：类比推理就是通过向量运算发现词汇间语义关系，比如“国王–男人+女人≈王后”。
公式表示为：

\[\text{vec}_{(king)} - \text{vec}_{(man)} + \text{vec}_{(woman)} \approx \text{vec}_{(queen)} \]

这是因为词嵌入向量空间可以捕捉语义方向，而同类关系的向量差几乎平行，因此通过向量运算就可以“举一反三”，我们便可以由此验证词嵌入的语义能力是否合理。
简单展开一下：

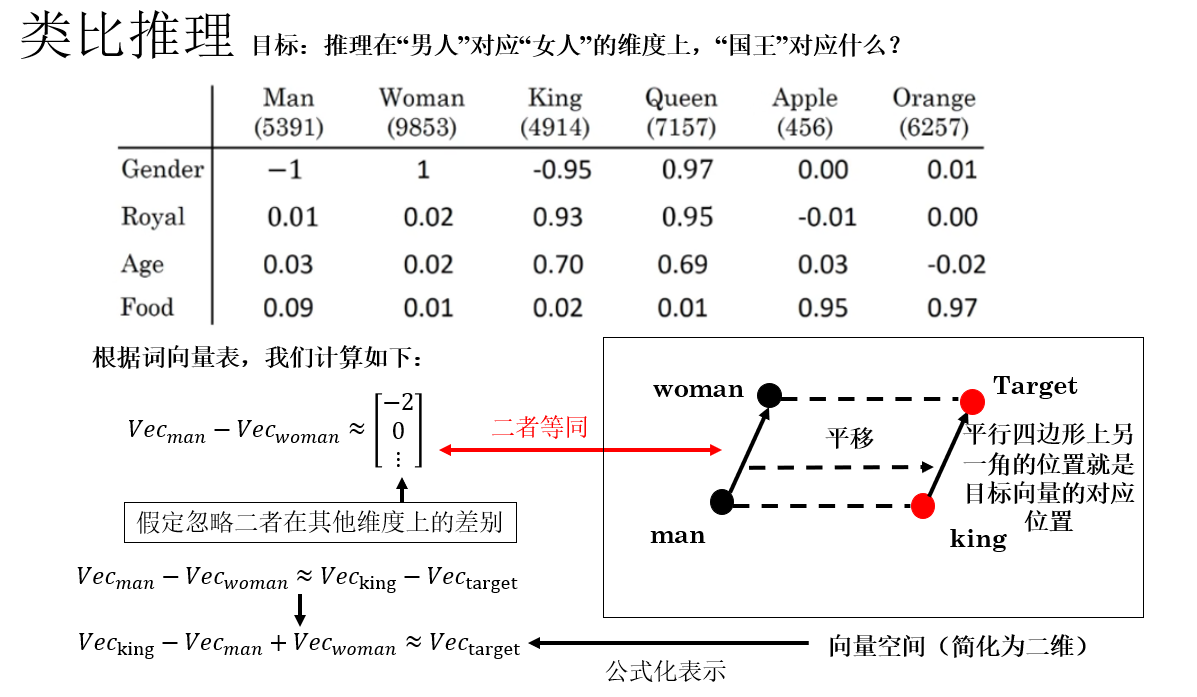
因此，你会发现，这部分计算：

\[\text{vec}_{(king)} - \text{vec}_{(man)} + \text{vec}_{(woman)} \]

实际上，是让‘国王’沿着‘男人→女人’的语义方向平移，以此来得到一个目标向量，如果词嵌入合理，那么这个向量就会指向语义上最接近“王后”的位置。

到这里，我们就得到了在男人对应女人的维度上，国王所对应的目标向量。
但是到这里还没有结束，我们还差一步，那就是找到在语义上距离目标向量最近的词向量，得到类比结果。
因此，我们下一步的工作就是将目标向量与词表中所有词向量逐个计算相似度，再选取相似度最高的词作为预测结果。

如何计算相似度？你可能会想到我们常用的欧氏距离。

\[d(\vec{x}, \vec{y}) = |\vec{x} - \vec{y}| = \sqrt{\sum_{i=1}^{d} (x_i - y_i)^2} \]

然而，在词嵌入空间中，直接使用欧氏距离并不是一个理想的选择。
这是因为欧氏距离同时受到向量方向和向量长度的影响，虽然词向量维度相同，但训练目标并不会约束不同词向量的长度一致。由于词频、梯度更新次数和优化路径的差异，不同词向量的范数往往不同，而这些长度差异并不一定对应语义差异。
听起来很复杂，来举个例子看看：

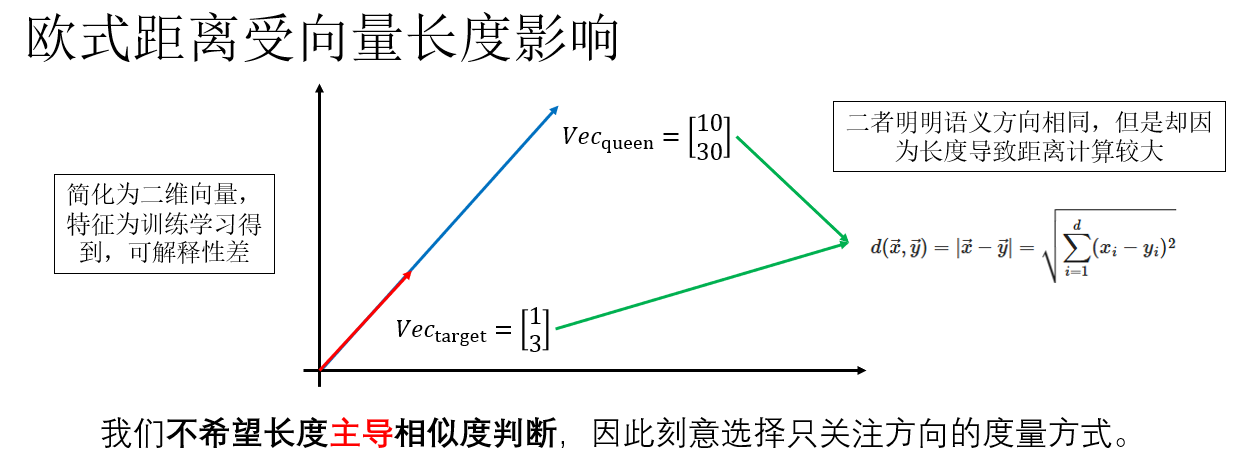
换句话说，在语义上非常接近的两个词向量，可能只是因为长度不同，在欧氏距离下被判定为“相距较远”，从而干扰类比推理的结果。
相比之下，我们更关心的是： 目标向量与某个词向量在语义方向上是否一致。
这正是余弦相似度（Cosine Similarity） 所度量的内容。
余弦相似度通过计算两个向量夹角的余弦值，来衡量它们在方向上的一致程度，其定义为：
其定义为：

\[\cos(\theta) = \frac{\vec{x} \cdot \vec{y}}{|\vec{x}| |\vec{y}|} = \frac{\sum_{i=1}^{d} x_i y_i}{\sqrt{\sum_{i=1}^{d} x_i^2} \sqrt{\sum_{i=1}^{d} y_i^2}} \]

其中，\(\vec{x} \cdot \vec{y}\) 表示向量的点积，\(|\vec{x}|\) 与 \(|\vec{y}|\) 分别表示向量的欧几里得范数（向量各维度平方和的开方）。
可以看到，余弦相似度在计算过程中对向量进行了长度归一化，因此最终的结果只与两个向量之间的夹角有关，而与它们的绝对长度无关。

从几何角度来看，余弦相似度实际上回答的是这样一个问题： “这两个向量指向的方向有多一致？”
当两个向量方向完全一致时，夹角 \(\theta = 0^\circ\)，此时 \(\cos(\theta)=1\)。
当两个向量正交时，\(\theta = 90^\circ\)，\(\cos(\theta)=0\)。
而当两个向量方向相反时，\(\theta = 180^\circ\)，\(\cos(\theta)=-1\)。
这与我们在词嵌入中的直觉是高度一致的： 如果两个词在语义空间中表达的是相似或相关的含义，那么它们的向量应当指向相近的方向，而语义无关的词，其向量方向往往接近正交。

我们仍然用前面的例子再来演示一下：

\[\vec{v}_{target} = [1, 3] ， \vec{v}_{queen} = [10, 30] \]

显然，这两个向量方向完全一致，仅长度不同。
计算它们的余弦相似度：

\[\cos(\theta) = \frac{1 \times 10 + 3 \times 30}{\sqrt{1^2 + 3^2} \cdot \sqrt{10^2 + 30^2}} = \frac{100}{\sqrt{10} \cdot \sqrt{1000}} = 1 \]

可以看到，尽管两个向量在欧氏距离下“相距很远”，但在余弦相似度的度量下，它们被正确地判定为语义方向完全一致。
因此，在词嵌入的类比推理任务中，我们通常采用余弦相似度来衡量目标向量与词表中各个词向量之间的接近程度，从而选取语义上最合理的预测结果。

我们会在之后的词嵌入模型中再展开为什么有些词向量的长度很大，而长度又代表了什么。
由此，我们完成了使用词嵌入来进行类比推理的过程，这不仅是词嵌入的一项应用，我们也可以用它来检验词嵌入模型对语义的理解能力。

3. 总结

概念	原理	比喻
词汇表征	将词汇表示为多维连续向量（词向量/embedding），以便模型计算和比较。	词汇像嵌入在高维空间里的点，距离反映语义相似性。
独热编码（One-hot）	每个词用高维稀疏向量表示，向量间互相正交。	每个词孤立存在，苹果和橘子、男人和女人没有联系。
词嵌入（Embedding）	将词向量映射到同一向量空间进行学习和比较，低维、连续、可度量相似性。	像把高维词汇空间“压缩”成一个连续空间，词语间距离反映语义。
类比推理	通过向量运算发现词汇间语义关系，公式：\(\vec{king}-\vec{man}+\vec{woman}\approx \vec{queen}\)	国王沿“男人→女人”的语义方向平移，指向王后。
相似度计算	欧氏距离受向量长度影响，可能误判语义；余弦相似度只看向量方向	方向一致的向量被判定语义相近，即使长度不同。
余弦相似度	$$\cos(\theta) = \frac{\vec{x} \cdot \vec{y}}{|\vec{x}| , |\vec{y}|}$$	两个向量方向一致就像箭头指向相同方向，即使箭头长短不同也一样。
向量长度	主要受词频、梯度累计等训练因素影响，不直接对应语义。	长度大不代表更“重要”，方向才决定语义关系。
可视化（t-SNE）	将高维词向量映射到2D/3D平面，尽量保留局部相似关系。	像把高维空间“摊平”，方便观察词语间距离。