DAG 定向是一个经典的集合划分容斥问题,我们想要做到每次删去一个 极大 的出度为零的点集,这个东西没有办法直接做到,所以我们考虑给每个集合分配一个容斥系数去做到,通过各种方式都可以得到 \((-1)^{|S|-1}\) 的容斥系数。
但是现有的大部分解释都忽略了这样的一个问题,我们删去一个点集的过程是有序的,删去一个集合后会形成一些新的可删点,这样会使得我们可能把本属于不同层的点集去划分到一个集合,显然这样的结构不符合我们前面只对同层之间考虑,而且划分之间还有顺序。
一下面一张图举例,这是我们本来划分成了这些层。
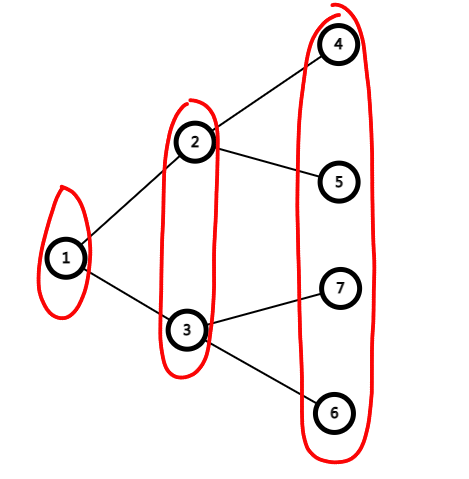
但是我们有可能会划分成如下结构。
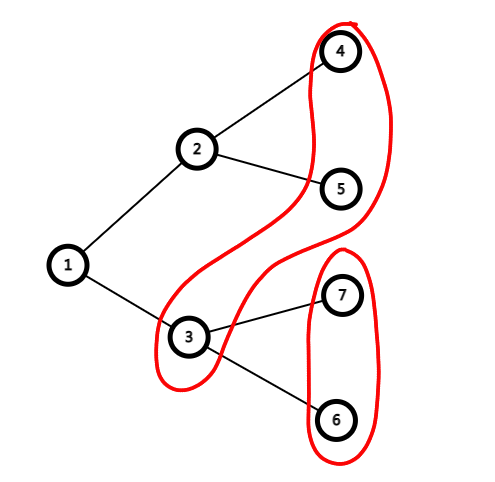
但是我们此时可以发现所有不符合一开始限制的划分的贡献都可以消去。考虑这样分析,我们对于一种删去方式我们找到最靠前的不符合限制的结构,这里有两种一个是把不同层的点划分到了一起,另一种是先删去更靠后的层的点。我们找到这样的位置,可以在此处把第一种的点集拆开就变成了第二种,把第二种的合并一下就可以对应回第一种,而且此时拆分出的集合数恰好差 1 ,就会有一个 -1 的系数,这样不合法的情况就可以两两消去,所以一开始的算法正确。