25 C++蓝桥杯B组题解
移动距离
题目大意:小明初始在二维平面的原点 (0,0),他想前往坐标 (233,666)。现在他有两种移动策略:
- 水平向右移动,即沿着 x 轴正方向移动一定的距离。
- 沿着一个圆心在原点 (0,0)、以他当前位置到原点的距离为半径的圆的圆周移动,移动方向不限(即顺时针或逆时针移动不限)。
【题解】:由于仅仅在水平方向的移动策略仅有 1 ,所以第一步显然只能执行 1 操作,最优操作一定是一次 1 操作然后一次 2 操作。
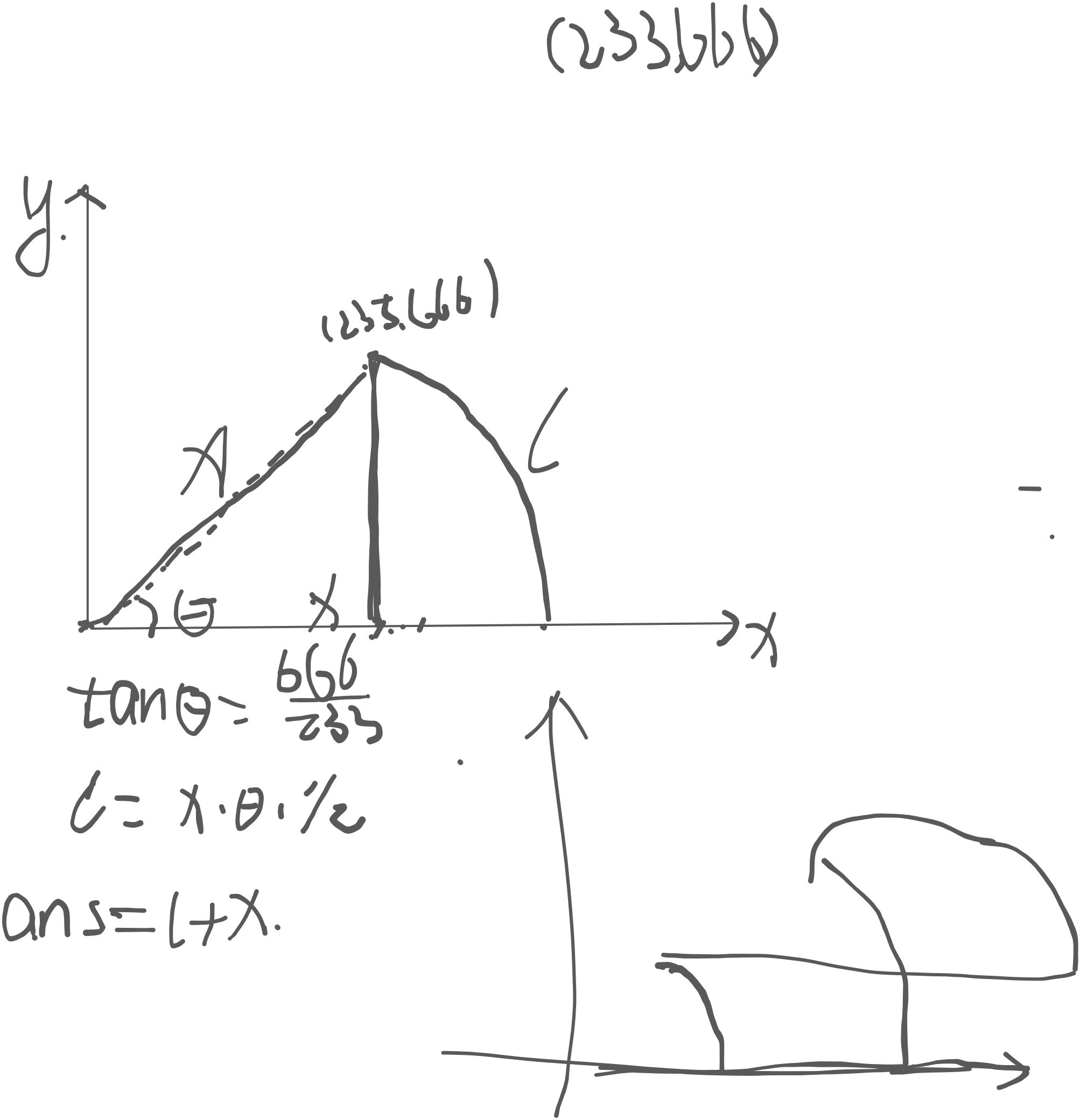
code:
#include <iostream>
#include <math.h>using namespace std;int main()
{double r = sqrt(233 * 233 + 666 * 666);double si = atan(666 * 1.0 / 233);cout << (int)(r + r * si + 0.5) << endl;return 0;
}
客流量上限
题目大意:求 1 - 2025 的排列,满足以下条件:对于认为位置 i,j $ i \le j $,选的数为 $ A_i,A_j
\(,\) $$ A_i * A_j \le ij + 2025 $。的排列的数量。
【题解】:由于对于一个 i ,j 的取值很多,这种题目暴力搜索显然是不可以的,就去尝试用题目给定的条件去缩小范围。
- 对于 i = j 的情况,$ A_i^2 \le i^2 + 2025 $-> $ A_i \le \sqrt{i^2 + 2025} $,其中 $ A_i $为整数。对于这个条件我们可以去进一步缩小 $ A_i $ 的取值情况。$ $
int main()
{for(int i = 1; i <= 2025; i++){cout << i << " " << (int)sqrt(i * i + 2025) << endl; }return 0;
}

我们会发现,在 $ i \ge 1013 \(,\) A_i \le i \(,此时我们把数分为两部分:\) i < 1013 \(,\) i > 1013 \(。根据上述结论,在\) i \ge 1013 \(的时候,由于前 1012 个数已经把数都用完了,对于这部分 i ,\) A_i = i $。
- 现在我们来讨论 $ i \le 1012 $ 的情况,这一部分的取值需要进一步去明确,我们取 $ i \le 1012, j \ge 1013 $。
-> $ A_i * j \le i * j + 2025 $ -> $ A_i \le i + \frac{2025}{j} = i+ 1 $。
- 对于 $ i= 1,A_i \le 2 $-> 两种选择方案;
- 对于 $ i= 2,A_i \le 3 $-> 两种选择方案;
- 对于 $ i= 3,A_i \le 4 $-> 两种选择方案;
.... -> $ ans = 2^{1012} %MOD $
code:
#include <iostream>
#include <cmath>using namespace std;
typedef long long LL;
const LL MOD = 1e9 + 7;LL qpow(LL a, LL b)
{LL ret = 1;while(b){if(b & 1) ret = ret * a % MOD;b >>= 1;a = a * a % MOD;}return ret;
}int main()
{cout << qpow(2, 1012) << endl;return 0;
}
可分解的正整数
题目大意:问一个正整数序列能够分解的数的个数,其中分解规则如下:- 分解成的序列长度要大于等于 3.
- 且分解的序列中的数字是连续递增的整数(可以为负数).
【题解】:显然对于一个非 1 的数都可以分解成 该数 + 一个和为 0 的递增前缀(-2 -1 0 1 2 3)。可以证明 1 不可分解。
code:
#include <iostream>using namespace std;int main()
{int n; cin >> n;int ans = 0;for(int i = 1; i <= n; i++){int x; cin >> x;if(x != 1) ans++;}cout << ans << endl;return 0;
}
产值调整
题目大意:对于给定三个初始值 A, B, C,问执行 k 次操作后最后的 A, B, C。每次操作: $ A^{'} = \frac{B + C}{2} $$ B^{'} = \frac{A + C}{2} $$ C^{'} = \frac{A + B}{2} $。
【题解】:我们可以模拟整个过程,但是 k 很大,会超时,发现在不断平均的过程中,A,B,C 最后会很快趋于一个定值,可以在模拟的时候判断一下。
#include <iostream>using namespace std;
typedef long long LL;void solve()
{LL a, b, c; cin >> a >> b >> c;LL k; cin >> k;while(k--){LL A = (b + c) / 2;LL B = (a + c) / 2;LL C = (a + b) / 2;if(A == a && B == b && C == c){break;}a = A;b = B;c = C;}````markdown<h1 id="zLLjO"><font style="color:#000000;">移动距离</font></h1>题目大意:<font style="color:rgb(36, 41, 46);">小明初始在二维平面的原点 (0,0),他想前往坐标 (233,666)。</font><font style="color:rgb(36, 41, 46);">现在他有两种移动策略:</font>1. <font style="color:rgb(36, 41, 46);">水平向右移动,即沿着 x</font>_<font style="color:rgb(36, 41, 46);"></font>_<font style="color:rgb(36, 41, 46);"> 轴正方向移动一定的距离。</font>2. <font style="color:rgb(36, 41, 46);">沿着一个圆心在原点 (0,0)、以他当前位置到原点的距离为半径的圆的圆周移动,移动方向不限(即顺时针或逆时针移动不限)。</font><font style="color:rgb(36, 41, 46);">【题解】:由于仅仅在水平方向的移动策略仅有 1 ,所以第一步显然只能执行 1 操作,最优操作一定是一次 1 操作然后一次 2 操作。</font>code:```cpp#include <iostream>#include <math.h>using namespace std;int main(){double r = sqrt(233 * 233 + 666 * 666);double si = atan(666 * 1.0 / 233);cout << (int)(r + r * si + 0.5) << endl;return 0;}```<h1 id="VBMxn"><font style="color:#000000;">客流量上限</font></h1>题目大意:求 1 - 2025 的排列,满足以下条件:对于位置 i, j <script type="math/tex">i \le j</script>,选的数为 <script type="math/tex">A_i, A_j</script>,且 <script type="math/tex">A_i A_j \le i j + 2025</script> 的排列的数量。【题解】:由于对于一个 i ,j 的取值很多,这种题目暴力搜索显然是不可以的,就去尝试用题目给定的条件去缩小范围。1. 对于 i = j 的情况,<script type="math/tex">A_i^2 \le i^2 + 2025</script> -> <script type="math/tex">A_i \le \sqrt{i^2 + 2025}</script>,其中 <script type="math/tex">A_i</script> 为整数。对于这个条件我们可以去进一步缩小 <script type="math/tex">A_i</script> 的取值情况。```cppint main(){for(int i = 1; i <= 2025; i++){cout << i << " " << (int)sqrt(i * i + 2025) << endl; }return 0;}```我们会发现,在 <script type="math/tex">i \ge 1013</script>,<script type="math/tex">A_i \le i</script>,此时我们把数分為两部分:<script type="math/tex">i < 1013</script>,<script type="math/tex">i > 1013</script>。根据上述结论,在 <script type="math/tex">i \ge 1013</script> 的时候,由于前 1012 个数已经把数都用完了,对于这部分 i,<script type="math/tex">A_i = i</script>。2. 现在我们来讨论 <script type="math/tex">i \le 1012</script> 的情况,这一部分的取值需要进一步去明确,我们取 <script type="math/tex">i \le 1012,\; j \ge 1013</script>。-> <script type="math/tex">A_i j \le i j + 2025</script> -> <script type="math/tex">A_i \le i + \frac{2025}{j} = i + 1</script>。- 对于 <script type="math/tex">i = 1,\; A_i \le 2</script> -> 两种选择方案;- 对于 <script type="math/tex">i = 2,\; A_i \le 3</script> -> 两种选择方案;- 对于 <script type="math/tex">i = 3,\; A_i \le 4</script> -> 两种选择方案;.... -> <script type="math/tex">ans = 2^{1012} \% MOD</script> code:```cpp#include <iostream>#include <cmath>using namespace std;typedef long long LL;const LL MOD = 1e9 + 7;LL qpow(LL a, LL b){LL ret = 1;while(b){if(b & 1) ret = ret * a % MOD;b >>= 1;a = a * a % MOD;}return ret;}int main(){cout << qpow(2, 1012) << endl;return 0;}```<h1 id="asriT">可分解的正整数</h1>题目大意:<font style="color:#000000;">问一个正整数序列能够分解的数的个数,其中分解规则如下:</font>1. 分解成的序列长度要大于等于 3.2. 且分解的序列中的数字是连续递增的整数(可以为负数).【题解】:显然对于一个非 1 的数都可以分解成 该数 + 一个和为 0 的递增前缀(-2 -1 0 1 2 3)。可以证明 1 不可分解。code:```cpp#include <iostream>using namespace std;int main(){int n; cin >> n;int ans = 0;for(int i = 1; i <= n; i++){int x; cin >> x;if(x != 1) ans++;}cout << ans << endl;return 0;}```<h1 id="zswDR">产值调整</h1>题目大意:对于给定三个初始值 A, B, C,问执行 k 次操作后最后的 A, B, C。每次操作:<script type="math/tex; mode=display">A' = \frac{B + C}{2}</script><script type="math/tex; mode=display">B' = \frac{A + C}{2}</script><script type="math/tex; mode=display">C' = \frac{A + B}{2}</script>【题解】:我们可以模拟整个过程,但是 k 很大,会超时,发现在不断平均的过程中,A,B,C 最后会很快趋于一个定值,可以在模拟的时候判断一下。```cpp#include <iostream>using namespace std;typedef long long LL;void solve(){LL a, b, c; cin >> a >> b >> c;LL k; cin >> k;while(k--){LL A = (b + c) / 2;LL B = (a + c) / 2;LL C = (a + b) / 2;if(A == a && B == b && C == c){break;}a = A;b = B;c = C;}cout << a << " " << b << " " << c << endl;}int main(){int t; cin >> t;while(t--) solve();return 0;}```<h1 id="画展布置">**<font style="color:rgb(36, 41, 46);">画展布置</font>**</h1>题目描述:给定一个长度为 n 的序列,从中选出 m 个,最小化这选择的 m 个数的 <script type="math/tex">\sum_{i=1}^{m - 1}\left| B_{i+1}^{2}-B_{i}^{2}\right|</script>。【题解】:显然当序列排序完成后,会包含最优解,此时双指针维护长度为 m 的区间中的上述值。code:```cpp#include <iostream>#include <vector>#include <algorithm>using namespace std;typedef long long LL;int main(){int n, k;cin >> n >> k;k--;vector<LL> a(n + 1);for(int i = 1; i <= n; i++) cin >> a[i];sort(a.begin(), a.end());LL ans = 1e18;LL sum = 0;int l = 2;for(int r = 2; r <= n; r++){sum += a[r] * a[r] - a[r - 1] * a[r - 1];while(r - l + 1 > k) {sum -= a[l] * a[l] - a[l - 1] * a[l - 1];l++;}if(r - l + 1 == k){ans = min(ans, sum);}}cout << ans << endl;return 0;}```<h1 id="lobmT">**<font style="color:rgb(36, 41, 46);">水质检测</font>**</h1>题目描述:在一个 2 * n 的矩形中,有若干连通块,我们需要找到将这些连通块全部联通的最小路径。【题解1】:01 BFS ,连接所有的连通块的最短路径,等于从最左边连通块走到最右边连通块的最短路,这是必然的,因为中途的连通块在最初始的连通块经过连通块的字符所在列的时候必然会联通该连通块。- 当下一个位置是 # 时,路径边权为 0.- 当下一个位置是 . 时,路径边权为 1.code:```cpp#include <iostream>#include <vector>#include <queue>#include <cstring>using namespace std;const int N = 1e6 + 10;int dist[2][N];deque<pair<int, int>> dq;char g[2][N];int n;int dx[] = {0, 0, 1, -1};int dy[] = {1, -1, 0, 0};int bfs(int i, int j){dist[i][j] = 0;dq.push_back({i, j});int ans = 0;while(dq.size()){auto [x, y] = dq.front(); dq.pop_front();for(int k = 0; k < 4; k++){int nx = x + dx[k];int ny = y + dy[k];if(nx < 0 || nx >= 2 || ny < 0 || ny >= n) continue;if(g[nx][ny] == '#') ans = max(ans, dist[nx][ny]);if(dist[nx][ny] != -1) continue;if(g[nx][ny] == '#') {dist[nx][ny] = dist[x][y];dq.push_front({nx, ny});}else {dist[nx][ny] = dist[x][y] + 1;dq.push_back({nx, ny});}}}return ans;}int main(){cin >> g[0] >> g[1];n = strlen(g[0]);memset(dist, -1, sizeof dist);for(int j = 0; j < n; j++){if(g[0][j] == '#'){cout << bfs(0, j) << endl;return 0;}if(g[1][j] == '#'){cout << bfs(1, j) << endl;return 0;}}return 0;}```````