省选模拟
CQXYM的线性规划
考虑到 \(x \in \{0,1\}\),显然并不能套用线性规划的做法。
观察到 \(a_i \leq b_i\),那么原限制相当于是对于所有 \(x_i=1\) 的物品,在 \([a_i,b_i]\) 区间内选一个数进行贡献,要求最后的贡献和 \(=p\)。
直接设 \(f_{i,j}\) 表示决策了前 \(i\) 个物品,当前总贡献为 \(j\),转移讨论当前物品选还是不选,以及具体的权值。
显然可以使用单调队列进行优化,总复杂度 \(O(nV)\)。
路径染色
观察数据范围和贡献形式不难猜出需要用费用流。
考虑先假设所有的路径都染成蓝色,然后把其中一部分转换成红色。
对于每条边原本至多有 \(r\) 条红色路径和 \(b\) 条蓝色路径的限制就转化为了形如每条边的红色路径条数必须处于区间 \([l,r]\) 内的限制。
考虑分别连边表示每条路径改变颜色还是不变,并利用树边处理区间限制,如下图:
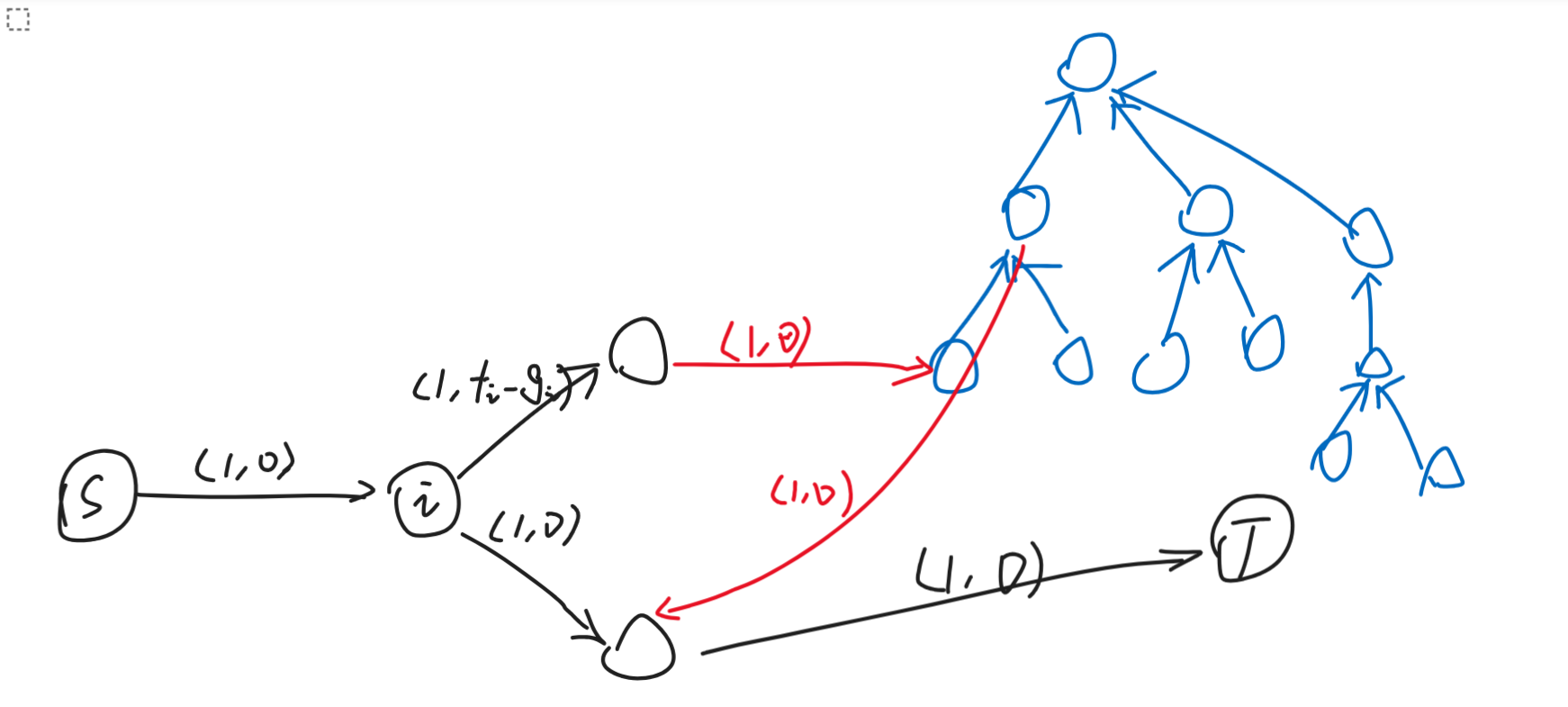
其中 \(f_i\) 和 \(g_i\) 分别表示第 \(i\) 条路径选红色和蓝色所造成的总贡献。
建出图后直接跑有源汇上下界最小费用最大流即可。