原题链接
区间修改
参考文献
董晓代码
@
- 前言
- 一、树状数组
- 树状数组与线段树的区别
- 树状数组单点修改
- 二、lowbit()实现传递点连接
- lowbit()的定义
- 为什么要用 lowbit() ?
- 三、树状数组里的差分
- 为什么用差分?
- 树状数组与差分结合
- 四、代码分析
- ac代码
- 逐步分析
- 输入数据
- add ( ) 函数
- query ( )函数
- 总结
前言
之前在其他平台上发过,现在完全转到博客园了就补一下:)
涉及关键知识点:树状数组,lowbit,差分,前缀和
与线段树相比,树状数组的优势是占用内存小,速度快。但树状数组相当于线段树的阉割版,所以相对于线段树是有一定局限性。我将会以 树状数组->lowbit->差分与前缀和->建立两个树状数组实现区间修改 来讲解
一、树状数组
树状数组与线段树的区别
蓝色区域为占用的内存
这是线段树的示意图
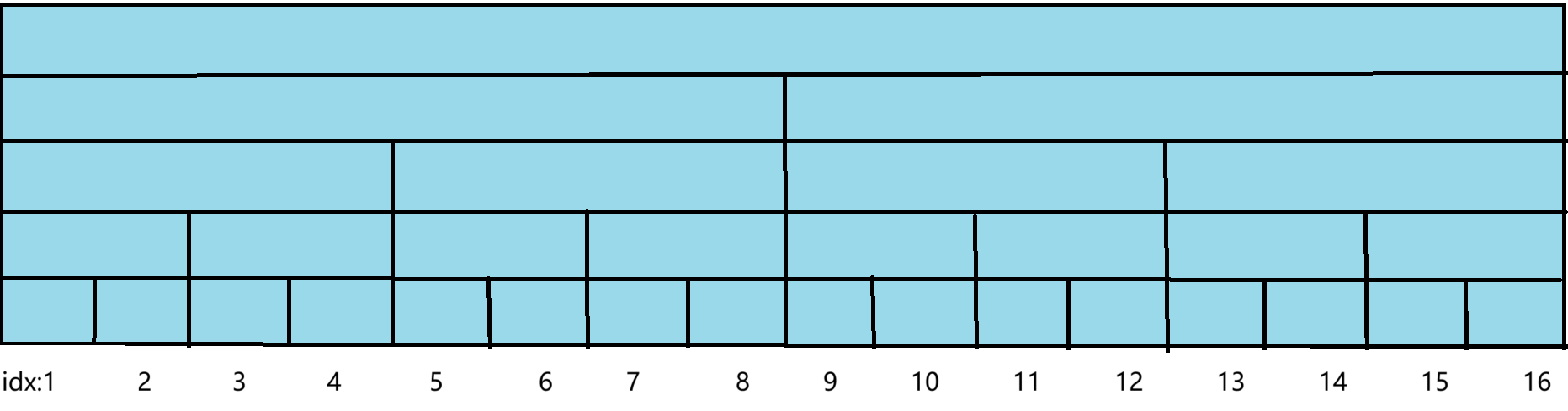
这是树状数组的示意图
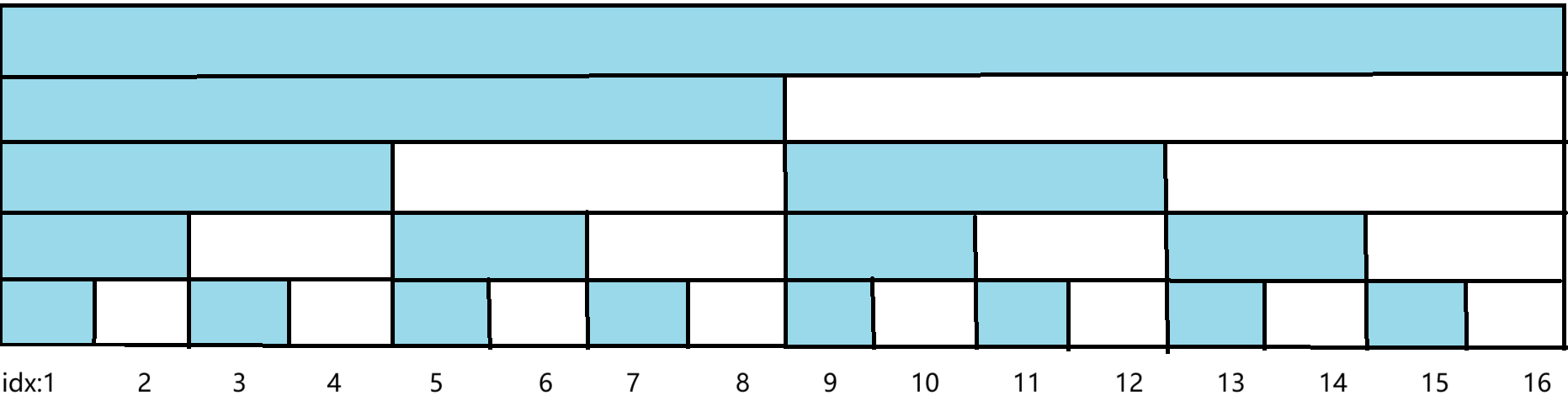
对比这两个图,我们能看出树状数组的内存占用小于线段树。接下来我们来看看为什么要舍弃一些点。
树状数组单点修改
我们先把树状数组下个定义
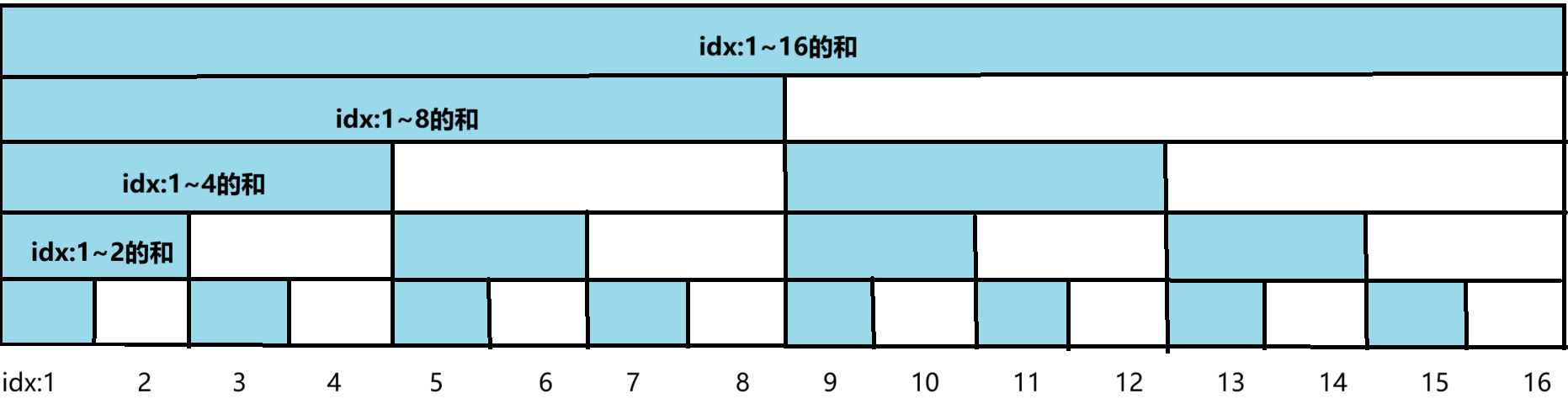
然后确定一下这些区间在数组里的位置
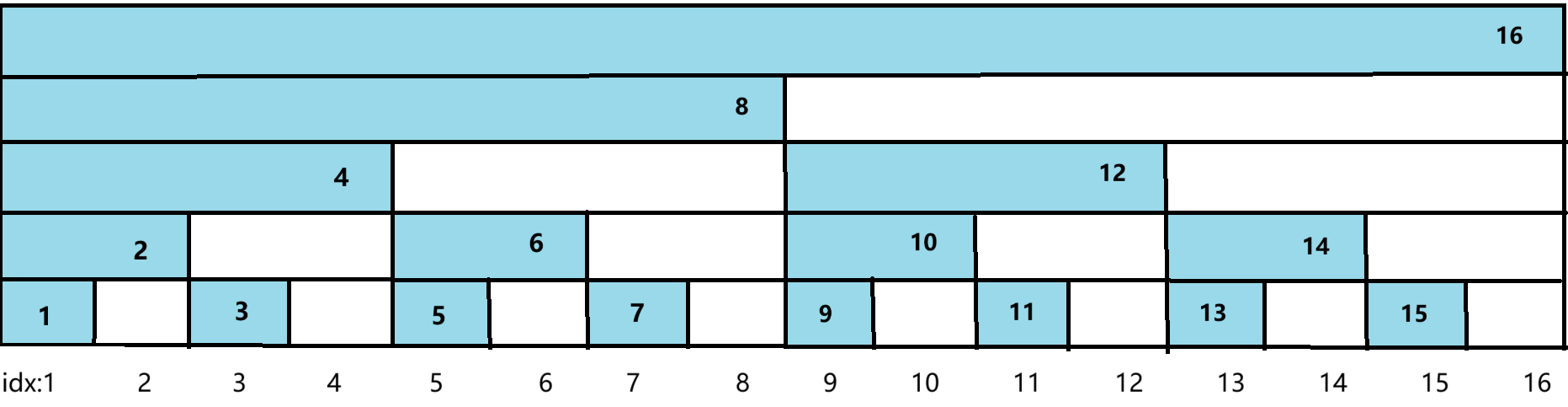
假如我们要修改 idx=3 位置的值,只要紧接着修改idx=4,8,16 的值就行了,所以我们要实现一个类似与线段树里push_up()函数的操作(向上传递值)。这时候我们就有一个疑问,把3,4,8,16这4个点联系起来呢?这时候要引入lowbit()的概念了
二、lowbit()实现传递点连接
lowbit()的定义
lowbit ( x ) 定义为非负整数 x 在二进制表示下 “ 最低位的 1 及其后面的所有的 0 ” 的二进制构成的数值。
单看定义肯定难理解,我们来举几个例子:
比如
3 的 二进制为 11 末尾的1 在 2^0 的位置上,所以 lowbit ( 3 ) = 1
4 的 二进制为 100 末尾的1 在 2^2 的位置上,所以 lowbit ( 4 ) = 4
6 的 二进制为 110 末尾的1 在 2^1 的位置上,所以 lowbit ( 6 ) = 2
为什么要用 lowbit() ?
再看看这张图

我们发现
3 到 4 满足 4 = 3 + lowbit ( 3 );
4 到 8 满足 8 = 4 + lowbit ( 4 );
我们可以得出一个结论:节点 x 与它的上级节点相差一个 lowbit( x );
lowbit ( )的写法也很简单
int lowbit(int x){return x&-x;
}
这样,我们就成功把这棵树连起来了!
不过,我们发现到此只能进行单点修改,并不能直接修改区间,这时候就该差分登场啦!
三、树状数组里的差分
为什么用差分?
很明显,我们发现在树状数组中只能点修改。那么该怎么实现只修改单个点就能表示出修改一个区间呢。这个时候差分就该出场了。
差分,就是把一个数拆成两个数的差,比如:
我们令 差分数组d [ i ] = a [ i ] - a [ i - 1 ];
那么 d [ 1 ] + d [ 2 ] + d [ 3 ] + ...+ d [ i ] = a [ i ];
这样,就能发现,如果我们要让a[ x ]到a[ y ]的值加 k ,只要让差分数组d[ x ] + k 和让 d[ y + 1 ] - k就行了。
比如:
我们要修改 idx = 3 到 5 的值加 k ,我们让d [ 3 ] + k 就代表 a [ 3 ] 开始到后面的 a [ n ] 都加上了 k;
而再令 d [ 6 ] - k 就代表a [ 6 ]开始到a [ n ]都减去k。
这样我们实际只变化了 a [ 3 ] 到 a [ 5 ] 而不改变其他点。
但是,如果单纯的用差分,虽然修改时间复杂度是 O( 1 ) ,但 查询却是 O( n ) 这个时候就是 树状数组 与 差分 结合了
树状数组与差分结合
如果我们要求 a [ 1 ] 到 a [ r ] 的区间和
注意,接下来可能有点绕
a [ 1 ] + a [ 2 ] + a [ 3 ] + ... + a [ r ]
= d [ 1 ] + ( d [ 1 ] + d [ 2 ] ) + ( d [ 1 ] + d [ 2 ] + d [ 3 ]) + ... + ( d [ 1 ] + d [ 2 ] + ... + d [ r ] )
= d [ 1 ] * r + d [ 2 ] * ( r - 1 ) + d [ 3 ] * ( r - 2 ) +...+ d [ r ]
= ( d [ 1 ] + d [ 2 ] + ... + d [ r ] ) * r - ( d [ 1 ] * 0 + d [ 2 ] * 1 + ... + d [ r ] * ( r - 1 ) )
我们化到这个样子就行了。
这时候,我们开 两棵树状数组 分别为 s1 存 d [ i ] 和 s2 存d [ i ] * ( i - 1 )
就能写出查询 x 到 y 的 区间和
sum = ( query ( s1 , y ) * y - query ( s2 , y ) ) - ( query ( s1 , x - 1 ) * ( x - 1 ) - query ( s2 , x - 1) )
前面 被减数是表示 1 ~ y 的和
后面 减数是 1 ~ x - 1 的和 ,总的求出 sum 就是 区间 x ~ y 的和;
接下来我们来看看代码该怎么写
四、代码分析
ac代码
我们先来看看ac代码,我们来逐步分析
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+5;
int n,m;
int a[N];int b[N];
int lowbit(int x){return x&-x;
}
void add(int *s ,int x,int k){while(x<=n){s[x]+=k;x+=lowbit(x);}
}
int query(int *s,int x){int t=0;while(x){t+=s[x];x-=lowbit(x);}return t;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=1;i<=n;i++){int k;cin>>k;add(a,i,k);add(a,i+1,-k);add(b,i,k*(i-1));add(b,i+1,-k*i);}while(m--){char op;int x,y,k;cin>>op;cin>>x>>y;if(op=='Q'){k=query(a,y)*y-query(b,y)-(query(a,x-1)*(x-1)-query(b,x-1));cout<<k<<"\n";}else{cin>>k;add(a,x,k);add(a,y+1,-k);add(b,x,k*(x-1));add(b,y+1,-k*y);}} return 0;
}
逐步分析
输入数据
for(int i=1;i<=n;i++){int k;cin>>k;add(a,i,k);add(a,i+1,-k);add(b,i,k*(i-1));add(b,i+1,-k*i);}
这里就是上面差分的运用, i 与 i + 1的区间修改,实际就是单点赋值操作
add ( ) 函数
void add(int *s ,int x,int k){while(x<=n){s[x]+=k;x+=lowbit(x);}
}
这边就是修改一个点之后向上传递,是前面lowbit ( ) 的运用
query ( )函数
int query(int *s,int x){int t=0;while(x){t+=s[x];x-=lowbit(x);}return t;
}
这边就是x向下找的知道找完,实际这是一个求前缀和的操作,也就是求 a [ x ] 。最后的 t 就是 a[ x ]的值
总结
树状数组就是把修改和查询的时间复杂度折中了一下,都变成O ( log(n) ) ,这让查询与修改的在保证效率的基础下能抵住极端的大量查询和大量修改