1.冒泡排序
1.1 基本概念
冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。这个算法的名称由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端(升序排列)。
1.2 算法步骤
- 比较相邻元素:从数组的第一个元素开始,比较相邻的两个元素
- 交换位置:如果第一个元素比第二个元素大(升序排列时),就交换它们的位置
- 重复遍历:对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数
- 缩小范围:针对所有的元素重复以上的步骤,除了最后一个
- 持续进行:持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较
1.3 时间复杂度分析
- 最好情况:当输入的数据已经是正序时,时间复杂度为O(n)
- 最坏情况:当输入的数据是反序时,时间复杂度为O(n²)
- 平均情况:时间复杂度为O(n²)
1.4 空间复杂度
冒泡排序的空间复杂度为O(1),因为它只需要一个额外的空间用于交换元素。
1.5 代码示例(java实现)
package com.heima;
import java.util.Arrays;
/*** 冒泡排序*/
public class BubbleSort {public static void bubbleSort(int[] arr) {for(int j=0;j< arr.length;j++){for (int i =0;i< arr.length-1;i++){if (arr[i] > arr[i+1]) {int temp = arr[i];arr[i]=arr[i+1];arr[i+1]=temp;}}}}public static void main(String[] args) {int[] arr = { 49, 38, 65, 97, 76, 13, 27, 1 };bubbleSort(arr);System.out.println(Arrays.toString(arr));}
}![]()
2.快速排序
2.1 递归算法
递归算法是一种通过函数调用自身来解决问题的编程方法。其核心思想是将一个大问题分解为若干个结构相似的小问题,直到达到可以直接求解的基准情形(base case)。
递归算法通常包含两个关键部分:
- 递归条件(Recursive Case):定义如何将问题分解为更小的子问题
- 基准条件(Base Case):定义可以直接求解的最简单情形,防止无限递
递归算法需要注意:
- 必须确保递归最终能到达基准条件
- 需要考虑栈空间限制,防止栈溢出
- 对于重复计算问题(如斐波那契数列),可以使用记忆化技术优化
递归与迭代的比较:
- 递归代码通常更简洁直观
- 迭代通常效率更高且不消耗额外栈空间
- 某些问题(如树遍历)用递归实现更自然
2.1.1 斐波那契数列
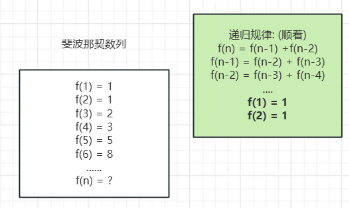
public static int sort(int n){if(n==1){return 1;}else if(n==2){return 1;}else{return sort(n-1)+sort(n-2);}
}2.2 快速排序(Quick Sort)
快速排序是一种高效的排序算法,采用分治策略(Divide and Conquer)进行排序。其核心思想是通过一次排序将待排序的数据分割成独立的两部分,其中一部分的所有数据都比另一部分的数据小,然后再递归地对这两部分数据进行排序。
2.2.1 算法步骤
- 选取数组第一个元素作为基准数,初始化i和j分别指向数组首尾两端
- j游标从右向左移动,寻找比基准数小的元素,找到后停止
- i游标从左向右移动,寻找比基准数大的元素,找到后停止
- 检查i和j是否相遇:
- 若未相遇,交换i和j指向的元素,重复步骤2-4
- 当i和j相遇时,交换相遇位置的元素与基准数
- 以基准数为界,将数组划分为左右两个子数组
- 递归地对子数组重复上述步骤,直到无法继续划分为止
2.2.2 示例代码(java实现,使用递归进行书写)
package com.heima;
import java.util.Arrays;
public class Demo {public static void sort(int arr[],int left,int right){if(left >= right)return;int base = arr[left];int i = left;int j = right;while(i < j){while(arr[j] >= base && i
2.2.3 时间复杂度
- 最优情况:每次分区都能将数组均匀分成两部分,时间复杂度为 (O(n \log n))。
- 最坏情况:每次分区都极不均匀(例如数组已经有序或逆序),时间复杂度为 (O(n^2))。
- 平均情况:时间复杂度为 (O(n \log n))。
2.2.4 空间复杂度
- 快速排序是原地排序算法,空间复杂度主要取决于递归调用的深度。最优情况下为 (O(\log n)),最坏情况下为 (O(n))。
2.2.5 应用场景
- 适用于大规模数据的排序,尤其是在内存有限的情况下。
- 常用于编程语言内置的排序函数(如Python的
list.sort()和sorted()函数)。
2.2.6 优缺点
- 优点:
- 平均性能优异,适合大多数场景。
- 原地排序,节省内存。
- 缺点:
- 最坏情况下性能较差。
- 递归实现可能导致栈溢出(可通过尾递归优化或迭代方式解决)。
3. 堆排序
堆排序(Heap Sort)是一种基于二叉堆(Binary Heap)数据结构的比较排序算法。它利用堆这种特殊的数据结构来实现高效的排序,具有稳定且良好的时间复杂度。
3.1 算法原理
堆排序的基本思想是将待排序的序列构造成一个大顶堆(或小顶堆),此时整个序列的最大值(或最小值)就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个序列重新构造成一个堆,这样会得到n个元素的次大值。如此反复执行,便能得到一个有序序列。
关键步骤:
构建堆(Heapify):将无序序列构建成一个堆,根据升序或降序需求选择大顶堆或小顶堆。
- 大顶堆:每个节点的值都大于或等于其子节点的值,用于升序排序
- 小顶堆:每个节点的值都小于或等于其子节点的值,用于降序排序
调整堆:将堆顶元素与末尾元素交换,缩小堆的范围,并重新调整堆结构
重复调整:重复步骤2直到整个序列有序
3.2 算法实现
堆排序的实现主要包含两个核心操作:
-
sort(int arr[],int parent,int length):创建大顶堆
main:调用sort函数创建大顶堆,使用循环经行堆排序
package com.heima;
import java.util.Arrays;
public class Duisort {public static void sort(int arr[],int parent,int length){int child = 2*parent+1;while(childarr[child]){child++;}if(arr[parent]=0;p--){sort(arr,p,length);}//堆排序for(int i=length-1;i>=0;i--){int temp = arr[0];arr[0]=arr[i];arr[i]=temp;sort(arr,0,i);}System.out.println(Arrays.toString(arr));}
}
3.3 复杂度分析
时间复杂度:
- 建堆过程:O(n)
- 每次调整堆:O(log n)
- 总体:O(n log n)(最好、最坏和平均情况都是如此)
空间复杂度:O(1)(原地排序)
3.4 特点与应用
优点:
- 时间复杂度稳定在O(n log n)
- 不需要额外的存储空间(原地排序)
- 适用于大数据量的排序
缺点:
- 不稳定排序(相同元素的相对位置可能改变)
- 在数据量较小时可能不如插入排序高效
- 缓存局部性较差(频繁的远距离元素交换)
3.5 与其他排序算法的比较
vs 快速排序:
- 堆排序最坏情况也是O(n log n),而快排最坏是O(n²)
- 但快排的常数因子通常更小,实践中往往更快
- 快排是稳定排序,堆排序不稳定
堆排序虽然在实际应用中不如快速排序使用广泛,但其稳定的时间复杂度使其在某些特定场景(如实时系统、内存受限环境)中具有独特优势。理解堆排序不仅有助于掌握重要的数据结构知识(堆),也是学习其他基于堆的算法(如Dijkstra算法、优先级队列等)的基础。